PythonでMCMC(メトロポリス法)-ベイズ統計学 [統計学]
最近は状態空間モデリングの勉強をしています。その一環できちんとMCMCを理解しようとあれこれ資料を漁っていました。マルコフ連鎖モンテカルロ法を実装してみようというブログ記事や「計算統計 2 マルコフ連鎖モンテカルロ法とその周辺 」などを読みつつ、メトロポリス法というシンプルなMCMCをPythonで実装してみました。
」などを読みつつ、メトロポリス法というシンプルなMCMCをPythonで実装してみました。
■計算条件
・2変量正規分布からサンプリング
【2変量正規分布】
=\frac{1}{Z}exp(-\frac{x_1^2-2bx_1x_2+x_2^2}{2}))

・b = 0.5 (ここでは適当にこの値にした)
・burn-in = 0
-サンプリングの挙動を確認するためバーンインは0とした
■Pythonコード
■結果
・2変量の動き
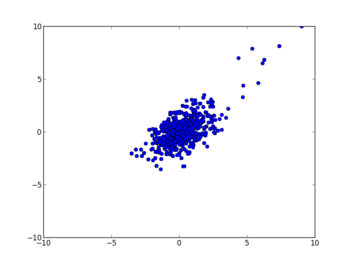
#初期値から数サンプルはふらふらと彷徨うが、しばらくすると最大値付近に収束
・p(x1,x2)の収束状況
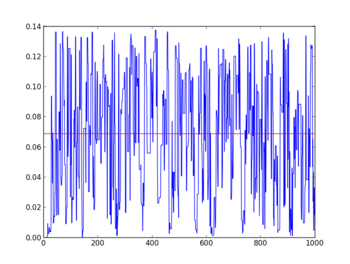
#時系列にグラフ化すると収束性を確認することができる
■感想
・メトロポリス法はとシンプルなアルゴリズムで理解しやすい
・この調子でメトロポリスヘイスティング法とギブスサンプラー法も理解する予定
・GAなんかを併用する手法はないのかな?
■参考文献

・伊庭先生の解説が一番分かりやすいと思う。これが少し難易度が高いなら久保先生のベイズ本 などを最初に読むといいです
などを最初に読むといいです
・あんまり注目されていないような気がするんだけど、この本も名著です。MCMCのRコードもあります。状態空間モデルのRコードはとても重宝しています。北川先生の時系列本 と合わせて読むと理解がより深まりますね!
と合わせて読むと理解がより深まりますね!
■計算条件
・2変量正規分布からサンプリング
【2変量正規分布】
・b = 0.5 (ここでは適当にこの値にした)
・burn-in = 0
-サンプリングの挙動を確認するためバーンインは0とした
■Pythonコード
#!/usr/bin/env python
#-*- coding:utf-8 -*-
import math
import random
import numpy as np
import matplotlib.pyplot as plt
def metropolis(func, start=10.0, delta=2.0, burn_in=0, seed=1):
metro_iter = _metropolis(func, start, delta, seed)
for i, value in enumerate(metro_iter):
if i > burn_in:
yield value
break
for value in metro_iter:
yield value
def _metropolis(func, start, delta, seed):
random.seed(seed)
initial_x1 = start
initial_x2 = start
initial_fx = func(initial_x1, initial_x2)
proposed_x1, proposed_x2, proposed_fx = 0.0, 0.0, 0.0
for j in range(1,1000):
proposed_x1 = initial_x1 + random.uniform(-delta, delta)
proposed_x2 = initial_x2 + random.uniform(-delta, delta)
proposed_fx = func(proposed_x1, proposed_x2)
ratio = proposed_fx / initial_fx
if ratio > 1.0 or ratio > random.random():
initial_x1, initial_x2, initial_fx = proposed_x1, proposed_x2, proposed_fx
yield proposed_x1, proposed_x2, proposed_fx
else:
yield initial_x1, initial_x2, initial_fx
def main():
b = 0.5
Z = 2*math.pi/math.sqrt(1.0-b**2.0)
f = lambda x1, x2: math.exp(-(x1**2-2*b*x1*x2+x2**2)/2)/Z
xb1 = []
xb2 = []
fxb1 = []
for x1, x2, fx in metropolis(f):
xb1.append(x1)
xb2.append(x2)
fxb1.append(fx)
tx = range(1,len(fxb1)+1)
md = [np.median(fxb1)]*(len(fxb1))
plt.plot(xb1,xb2,"bo")
plt.axis([-10, 10, -10, 10])
plt.show()
plt.plot(tx, fxb1)
plt.plot(tx, md, "r")
plt.axis([0, 1000, 0, 0.14])
plt.show()
if __name__ == '__main__':
main()
■結果
・2変量の動き

#初期値から数サンプルはふらふらと彷徨うが、しばらくすると最大値付近に収束
・p(x1,x2)の収束状況

#時系列にグラフ化すると収束性を確認することができる
■感想
・メトロポリス法はとシンプルなアルゴリズムで理解しやすい
・この調子でメトロポリスヘイスティング法とギブスサンプラー法も理解する予定
・GAなんかを併用する手法はないのかな?
■参考文献

計算統計 2 マルコフ連鎖モンテカルロ法とその周辺 (統計科学のフロンティア 12)
- 作者: 伊庭 幸人
- 出版社/メーカー: 岩波書店
- 発売日: 2005/10/27
- メディア: 単行本
・伊庭先生の解説が一番分かりやすいと思う。これが少し難易度が高いなら久保先生のベイズ本
・あんまり注目されていないような気がするんだけど、この本も名著です。MCMCのRコードもあります。状態空間モデルのRコードはとても重宝しています。北川先生の時系列本
2013-03-22 19:00
nice!(0)
コメント(0)
トラックバック(0)





コメント 0